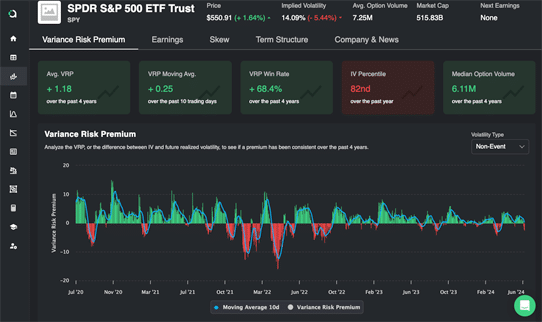
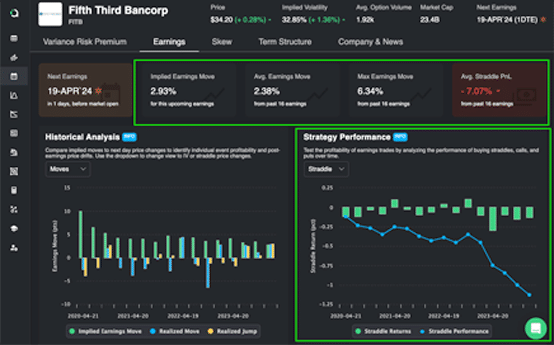
When I first learned that volatility and time were the same thing it was pretty mind blowing. It changed the way I think about how options reflect the implied volatility for a ticker over time. In this article we are going to cover how volatility is actually synthetic time and walk through an example of how this impacts option prices.
Once you understand that volatility is the same thing as synthetic time, you can start to really understand how structure like calendar spreads work and how changes in the term structure can be measured and forecasted. It unlocks and entirely new world of trading that 99% of retail option sellers don’t even know exist.
Key Takeaways
- Volatility as Synthetic Time: Higher implied volatility (IV) compresses time by increasing the range of potential daily price movements. This makes options behave as if they have more time until expiration, reducing theta (time decay) and gamma (rate of change of delta).
- Practical Application – Earnings Trades: Understanding this concept helps explain the behavior of options around earnings events. For example, if IV spikes before an earnings announcement, options behave like they have more days to expiration, showing less sensitivity to daily movements. This is why even though we see low realized volatility before the event (compared to implied) we do not realize much returns until the event passes.
This is an idea that really needs to be broken down so these key takeaways probably don’t make much sense right now. They will by the time you finish this article. Let’s jump into it!
The Concept of Volatility as Synthetic Time
Imagine a stock that can only move up or down by 1% each day. For example, if a stock can move up or down 1% daily, over 30 days, this results in an annualized IV of about 16%.
When the movement is defined as 1% daily, this is equal to an implied volatility of 16%.
With 1% daily moves, where could the stock end up in 4 days?
To visualize this, we construct a binomial tree, which shows us the range of possible moves.
If we examine a 4 day time period, we can see that the stock will end up in a range between +4% to -4% from its current value.
If we doubled the volatility, how long would it take to be +/- 4% from the current stock price?
Under the current assumption of 1% daily moves (16% implied volatility) it took 4 days for the stock to be +/- 4% from its current price. If we adjusted the volatility to be 2% daily moves (32% implied volatility), how long would it take to see the same range of moves?
Instead of taking four days, it only took two days for us to get to the same point!
When we double the volatility, the time to realize the same range is cut in half.
Because of this, increasing time or increasing volatility has the same impact on the value of an option.
Does that make sense? The reason that time and volatility can be thought of equal to each other is because they both change the range of potential moves that a stock can experience. They both result in the same impact on the underlying.
Practical Demonstration
Understanding volatility and its relationship to time helps us explain the way an option changes in value. A good example of this is when a ticker has an earnings event coming up. Meaning, when a ticker has some days of “non-event volatility” priced into their options, plus a single day with a much larger implied move (the earnings day).
Something important to note about the image above is that even though there are 30 days to expiration, the theta for each day is not evenly distributed.
This explains why we see such little change in option values as the earnings event approaches, and such a massive change after the event has passed.
The anticipation of significant stock movement around the earnings event causes IV for the entire expiration to spike, making the options behave as if they have more time until expiration. The option decays slowly.
Once the event has passed, that “12% day” in the image above is no longer priced into the chain, meaning that the implied volatility decreases drastically, which is equivalent to time decreasing. As such, the option returns to its regular theta decay as you would expect from an option on this ticker with this many days to expiration.
Applying Volatility as Synthetic Time to Earnings Trades
Real-World Example: Netflix
Let’s consider a real-world example involving Netflix (NFLX). One of our community members, Ronald, sold volatility on Netflix 10 days before its earnings announcement. Despite having a lot of short volatility exposure, his profit and loss (P&L) barely moved, fluctuating by only small amounts daily as the event approached. Until he understood the concept of volatility as synthetic time, he wasn’t able to piece together.
Ronald’s Netflix trade involved a short straddle, which is long theta and short gamma. If the volatility was evenly distributed across the expiration, it should have been realizing some returns. But since the implied volatility remained elevated due to all of the movement being concentrated on the earnings date, there was very little change to the value of his position. As a result, the options behaved more like longer-dated ones, showing less sensitivity to daily movements, hence the minimal daily P&L changes.
Conclusion
Once you understand that volatility is the same thing as synthetic time, you can start to really understand how structure like calendar spreads work and how changes in the term structure can be measured and forecasted. It unlocks and entirely new world of trading that 99% of retail option sellers don’t even know exist.
It’s powerful, so let’s put it to good use and find some alpha!